
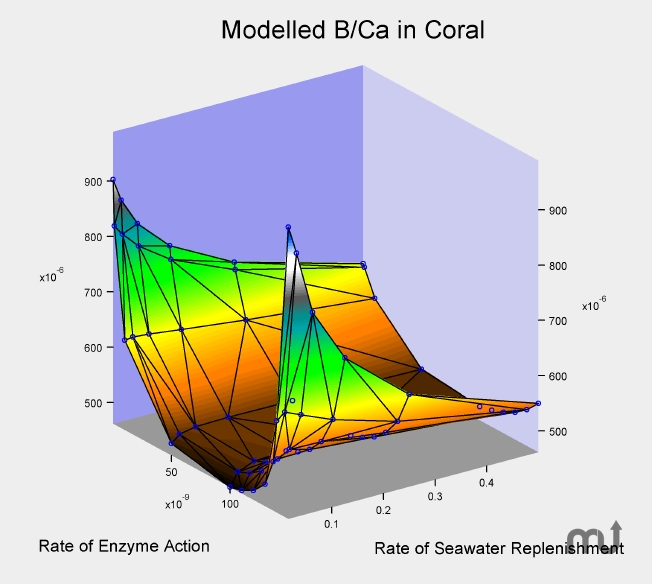
#Igor pro round number to 0.1 code
Let’s see the code below to observe how each of these functions work: import randomįirst, we import the decimal module. ROUND_UP: rounded values move away from 0.ROUND_HALF_UP: rounded values move halfway away from 0.ROUND_HALF_EVEN: rounded values move halfway to the nearest even number.ROUND_HALF_DOWN: rounded values move halfway towards 0.ROUND_FLOOR: rounded value is less than the number.ROUND_DOWN: rounded values moves towards 0.ROUND_CEILING: rounded value is greater than the number.This module offers many rounding strategies: Therefore, it preserves significant digits, gives a more exact representation of decimals, and allows for flexible precision as per the user’s convenience. It was designed by considering how people do arithmetic in real life. Python offers a decimal module which allows for more precision when dealing with numbers. To make it clearer, let’s look at the code below. If you want to round up numbers, you only need to include the first argument in round(), i.e., the value on which you want to perform the function.įor decimals greater than 0.5, round() always returns the higher integer value.įor example, if you were rounding off 10.6 using round(), the Python interpreter will display 11. It takes two values as arguments the number “n” that is to be rounded off and “i,” the number of decimal places the number needs to be rounded off to. The first approach anyone uses to round numbers in Python is the built-in round function – round(n, i). In Python, there are two ways to round up numbers: Rounding up using round() It reduces the precision of your work but also makes calculation simpler. Rounding up numbers in decimal form means converting them to an integer greater than that number.
A lot of precision is lost when we use truncate instead of round(), which could lead to substantial problems. The output shows a significant difference between both strategies.
These are in the range of 500,000 seconds. We’ve imported the random library, using which we’ve initiated an array of random numbers between 0.01 and 0.1 using random.uniform().Let’s break the code down to make it more comprehensive: Print("Difference (round()) = ", sumOfNumbers1 - sumOfTruncate1) Print("Total Using round() = ", sumOfTruncate1) SumOfTruncate1 = round(sumOfTruncate1 + n, 3) Print("Using round() upto 3 decimal places:") Print("Difference (truncate) = ", sumOfNumbers - sumOfTruncate, '\n') Print("Total Using Truncate = ", sumOfTruncate) Print("Truncating upto 3 decimal places:") SumOfTruncate = truncateNumber(sumOfTruncate + n) Let’s consider the following code: import random The Vancouver Stock Exchange (VSE) is infamous for losing 25 points every month in 1982 because they truncated values to three decimal places several times each day. An example of a stock market clarifies things much more. Of course, this can make a massive difference when there are minor differences in values. Meanwhile, truncation discards the digits after the number of decimal places specified without considering any conditions. Rounding approximates a value to the nearest number, which simplifies calculations while preserving precision to some extent.


 0 kommentar(er)
0 kommentar(er)
